blog

How do you do 3 digit by 3 digit multiplication?

Photo of admin adminJanuary 15, 2024
0 28 12 minutes read
3 digit multiplication

Mastering (three)- 3 digit multiplication is a valuable skill that can enhance your mathematical abilities. By breaking down the process into manageable steps and practicing regularly, you’ll become proficient in solving these types of multiplication problems.

3 digit multiplication refers to the process of multiplying two numbers, each consisting of three digits. It involves multiplying the digits in each place value and carrying over any resulting values to the next place value. The result of a three-digit multiplication is a six-digit product. For example, multiplying 234 by 567 would be considered a three-digit multiplication.

This article will cover three types of three-digit multiplication: multiplying a three-digit number by a one-digit number, multiplying a three-digit number by a two-digit number, and multiplying a three-digit number by another three-digit number. We will provide examples and explanations to help you grasp these concepts more effectively.

What is 3-Digit Multiplication?

Three-digit multiplication involves multiplying a three-digit number with another number. The process begins by arranging the numbers in columns based on their place values (ones, tens, and hundreds). The larger number is placed on top as the multiplicand, while the smaller number is written below as the multiplier. Starting from the rightmost digit, the multiplier is multiplied with each digit of the multiplicand sequentially, moving from ones to tens and then hundreds. The products obtained are then combined to form the final product. This method ensures that each digit is multiplied and contributes to the overall result. By following this step-by-step process, three-digit multiplication can be performed accurately and efficiently.

To illustrate three-digit multiplication, let’s consider the example of multiplying 123 by 3. We arrange the numbers as follows, with 123 as the multiplicand and 3 as the multiplier. After performing the multiplication, the resulting product is 269.

Introduction: 3-digit multiplication
Multiplication is a fundamental mathematical operation, and mastering three-digit multiplication can greatly enhance your computational skills. In this blog post, we will provide a comprehensive guide on how to effectively tackle three-digit multiplication problems. By following these step-by-step instructions, you’ll gain confidence and proficiency in solving these types of multiplication equations.

  1. Understand Place Value:
    Before diving into three-digit multiplication, it’s crucial to have a solid understanding of place value. Review the concept of ones, tens, hundreds, and thousands, as this knowledge will form the foundation for solving three-digit multiplication problems.
  2. Break It Down:
    To simplify the process, break down the three-digit numbers into their individual place values. For example, consider 234 as 200 + 30 + 4 and 567 as 500 + 60 + 7.
  3. Multiply Digit by Digit:
    Starting from the rightmost digit, multiply each digit of the second number by each digit of the first number. Begin with one’s place and move leftward.
  4. Carry Over:
    If the product of two digits in one column exceeds 9, carry over the tenth digit to the next column. Ensure you keep track of these carried-over values during the process.
  5. Add the Partial Products: After multiplying each digit, add the partial products together, taking into account any carried-over values from step 4.
  6. Verify and Practice:
    To solidify your understanding, verify your solution by using a calculator or working backward to perform the division operation. Additionally, practice solving various three-digit multiplication problems to improve your speed and accuracy.

How to do 3-digit by 3 digit multiplication

How to do 3 digit by 3 digit multiplication

To perform three-digit by three-digit multiplication, you can follow these steps:

  1. Write the two three-digit numbers vertically, aligning them by place value. 
       123   <- Three-digit number
x  456   <- Another three-digit number
------
  2. Starting with the rightmost digit of the bottom number (the one’s place), multiply it by each digit of the top number, and write the partial products beneath each corresponding digit of the top number. 
       123   
x  456   
------
   738   <- Partial product (ones place)
  3. Move to the next digit of the bottom number (the tens place) and repeat the process, but shift each partial product one place to the left. 
       123   
x  456   
------
  738    <- Partial product (ones place)
 615     <- Partial product (tens place)
  4. Repeat the process for the leftmost digit of the bottom number (the hundreds place), shifting each partial product two places to the left. 
       123   
x  456   
------
  738    <- Partial product (ones place)
 615     <- Partial product (tens place)
+492      <- Partial product (hundreds place)
------
  5. Add up all the partial products to get the final result. 
       123   
x  456   
------
 56088   <- Final result
------

Remember to carry over any values that exceed nine during the multiplication process. The example provided demonstrates the steps for multiplying 123 by 456.

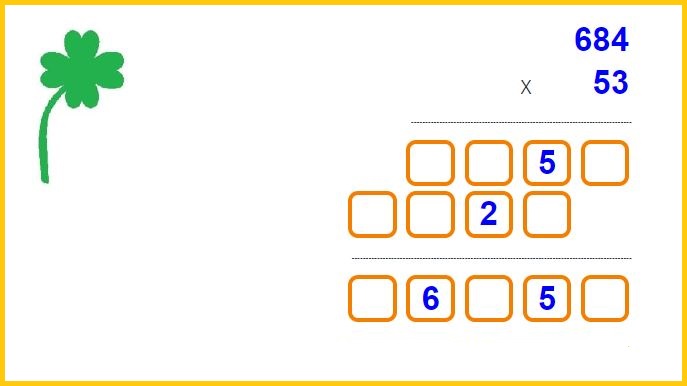
3 digit by 2 digit multiplication

3 digit by 3 digit multiplication

To multiply a three-digit number by a two-digit number, follow these steps:

  1. Write the two numbers vertically, aligning them by place value.
    asciidoc

       123   <- Three-digit number
x   45   <- Two-digit number
------
  2. Starting from the rightmost digit of the bottom number (the one’s place), multiply it by each digit of the top number, and write the partial products beneath each corresponding digit of the top number. 
       123   
x   45   
------
    615   <- Partial product (ones place)
  3. Move to the next digit of the bottom number (the tens place) and repeat the process, but shift each partial product one place to the left. 
       123   
x   45   
------
   615   <- Partial product (ones place)
 492    <- Partial product (tens place)
  4. Add up all the partial products to get the final result. 
       123   
x   45   
------
   615   <- Partial product (ones place)
 +492    <- Partial product (tens place)
------
  5535   <- Final result
------

In this example, we multiplied 123 by 45 to get a final result of 5535.

3 digit multiplication worksheets

Here are a few examples of three-digit multiplication worksheets:

Worksheet 1:

   123
x  456
------

Worksheet 2:

   789
x  567
------

Worksheet 3:

   234
x  678
------

Worksheet 4:

   456
x  789
------

Worksheet 5:

   567
x  123
------

You can print out these worksheets and solve them by following the steps mentioned earlier. Remember to align the numbers properly and carry over any values that exceed nine during the multiplication process.

How do you do 3 digit by 3 digit multiplication?

To multiply a three-digit number by another three-digit number, you can follow these steps:

  1. Write the two three-digit numbers vertically, aligning them by place value. 
       123   <- Three-digit number
x  456   <- Another three-digit number
------
  2. Starting with the rightmost digit of the bottom number (the one’s place), multiply it by each digit of the top number, and write the partial products beneath each corresponding digit of the top number. 
       123   
x  456   
------
   738   <- Partial product (ones place)
  3. Move to the next digit of the bottom number (the tens place) and repeat the process, but shift each partial product one place to the left. 
       123   
x  456   
------
  738    <- Partial product (ones place)
 615     <- Partial product (tens place)
  4. Repeat the process for the leftmost digit of the bottom number (the hundreds place), shifting each partial product two places to the left. 
       123   
x  456   
------
  738    <- Partial product (ones place)
 615     <- Partial product (tens place)
+492      <- Partial product (hundreds place)
------
  5. Add up all the partial products to get the final result. 
       123   
x  456   
------
 56088   <- Final result
------

Remember to carry over any values that exceed nine during the multiplication process. The example provided demonstrates the steps for multiplying 123 by 456.

3 digit by 1 digit multiplication

To multiply a three-digit number by a one-digit number, you can follow these steps:

  1. Write the three-digit number and the one-digit number vertically, aligning them by place value. 
       123   <- Three-digit number
x   7   <- One-digit number
------
  2. Starting from the rightmost digit of the top number (the ones), multiply it by the one-digit number and write the product beneath it. 
       123   
x   7   
------
      3   <- Product (ones place)
  3. Move to the next digit of the top number (the tenth place) and repeat the process. 
       123   
x   7   
------
     21   <- Product (tens place)
  4. Repeat the process for the leftmost digit of the top number (the hundreds). 
       123   
x   7   
------
    861   <- Product (hundreds place)
  5. Add up the products to get the final result. 
       123   
x   7   
------
   861   <- Final result
------

In this example, we multiplied 123 by 7 to get a final result of 861.

Multiply by 3-digit numbers

To multiply a number by a three-digit number, you can use the traditional long multiplication method. Here’s how you can do it:

Let’s say you want to multiply a three-digit number, let’s call it “ABC,” by another three-digit number, let’s call it “DEF.”

  1. Write the numbers vertically, aligning them by place value.
    ABC
 x  DEF
 ------
  1. Start with the rightmost digit of the bottom number (the one place, “F”), and multiply it by each digit of the top number. Write the partial products beneath each corresponding digit of the top number, shifted to the right according to their place value.
    ABC
 x  DEF
 ------
    X   <- Partial product (ones place)
   XX    <- Partial product (tens place)
  XXX     <- Partial product (hundreds place)
  1. Move to the next digit of the bottom number (the tens place, “E”), and repeat the process. Multiply it by each digit of the top number, and write the partial products beneath each corresponding digit of the top number, shifted to the right according to their place value.
    ABC
 x  DEF
 ------
    X   <- Partial product (ones place)
   XX    <- Partial product (tens place)
  XXX     <- Partial product (hundreds place)
+XXXXX    <- Partial product (thousands place)
  1. Repeat the process for the leftmost digit of the bottom number (the hundreds place, “D”). Multiply it by each digit of the top number, and write the partial products beneath each corresponding digit of the top number, shifted to the right according to their place value.
    ABC
 x  DEF
 ------
    X   <- Partial product (ones place)
   XX    <- Partial product (tens place)
  XXX     <- Partial product (hundreds place)
+XXXXX    <- Partial product (thousands place)
------
  RESULT   <- Final result
  1. Add up all the partial products to get the final result.

Make sure to carry over any values that exceed nine during each step of the multiplication process.

Note: Replace “ABC” and “DEF” with the actual digits of the numbers you are multiplying.

Multiply 3 digit by 1 digit

To multiply a three-digit number by a one-digit number, you can use the traditional long multiplication method. Here’s how you can do it:

Let’s say you want to multiply a three-digit number, let’s call it “ABC”, by a one-digit number, let’s call it “D”.

  1. Write the numbers vertically, aligning them by place value.
    ABC
 x   D
 ------
  1. Start with the rightmost digit of the top number (the one place, “C”), and multiply it by the one-digit number. Write the product beneath the line.
    ABC
 x   D
 ------
     X   <- Product (ones place)
  1. Move to the next digit of the top number (the tenth place, “B”), and repeat the process. Multiply it by the one-digit number and write the product beneath the line, shifting one place to the left.
    ABC
 x   D
 ------
    XX   <- Product (tens place)
  1. Repeat the process for the leftmost digit of the top number (the hundreds place, “A”). Multiply it by the one-digit number and write the product beneath the line, shifting two places to the left.
    ABC
 x   D
 ------
   XXX  <- Product (hundreds place)
  1. Add up all the products to get the final result.
    ABC
 x   D
 ------
   XXX  <- Product (hundreds place)
  XX    <- Product (tens place)
 X      <- Product (ones place)
 ------
 RESULT <- Final result

Make sure to carry over any values that exceed nine during each step of the multiplication process.

Note: Replace “ABC” and “D” with the actual digits of the numbers you are multiplying.

Multiply 3-digit multiplication

To multiply two three-digit numbers, you can use the traditional long multiplication method. Here’s how you can do it:

Let’s say you want to multiply a three-digit number, let’s call it “ABC,” by another three-digit number, let’s call it “DEF.”

  1. Write the numbers vertically, aligning them by place value.
    ABC
 x  DEF
 ------
  1. Start with the rightmost digit of the top number (the one place, “C”), and multiply it by each digit of the bottom number. Write the partial products beneath each corresponding digit of the top number, shifted to the right according to their place value.
    ABC
 x  DEF
 ------
    X   <- Partial product (ones place)
   XX    <- Partial product (tens place)
  XXX     <- Partial product (hundreds place)
  1. Move to the next digit of the top number (the tens place, “B”), and repeat the process. Multiply it by each digit of the bottom number and write the partial products beneath each corresponding digit of the top number, shifted to the right according to their place value.
    ABC
 x  DEF
 ------
    X   <- Partial product (ones place)
   XX    <- Partial product (tens place)
  XXX     <- Partial product (hundreds place)
+XXXXX    <- Partial product (thousands place)
  1. Repeat the process for the leftmost digit of the top number (the hundreds place, “A”). Multiply it by each digit of the bottom number and write the partial products beneath each corresponding digit of the top number, shifted to the right according to their place value.
    ABC
 x  DEF
 ------
    X   <- Partial product (ones place)
   XX    <- Partial product (tens place)
  XXX     <- Partial product (hundreds place)
+XXXXX    <- Partial product (thousands place)
------
  RESULT   <- Final result
  1. Add up all the partial products to get the final result.

Make sure to carry over any values that exceed nine during each step of the multiplication process.

Note: Replace “ABC” and “DEF” with the actual digits of the numbers you are multiplying.

Multiply 3 digit by 1 digit

To multiply a three-digit number by a one-digit number, you can use the traditional long multiplication method. Here’s how you can do it:

Let’s say you want to multiply a three-digit number, let’s call it “XYZ,” by a one-digit number, let’s call it “W”.

  1. Write the numbers vertically, aligning them by place value.
    XYZ
 x   W
 ------
  1. Start with the rightmost digit of the top number (the ones place, “Z”), and multiply it by the one-digit number. Write the product beneath the line.
    XYZ
 x   W
 ------
     P   <- Product (ones place)
  1. Move to the next digit of the top number (the tenth place, “Y”), and repeat the process. Multiply it by the one-digit number and write the product beneath the line, shifting one place to the left.
    XYZ
 x   W
 ------
    PP   <- Product (tens place)
  1. Repeat the process for the leftmost digit of the top number (the hundreds place, “X”). Multiply it by the one-digit number and write the product beneath the line, shifting two places to the left.
    XYZ
 x   W
 ------
   PPP  <- Product (hundreds place)
  1. Add up all the products to get the final result.
    XYZ
 x   W
 ------
   PPP  <- Product (hundreds place)
  PP    <- Product (tens place)
 P      <- Product (ones place)
 ------
 RESULT <- Final result

Make sure to carry over any values that exceed nine during each step of the multiplication process.

Note: Replace “XYZ” and “W” with the actual digits of the numbers you are multiplying.

Multiplying 4 digits by 3 digits

how to do 3 digit by 2 digit multiplication

To multiply a four-digit number by a three-digit number, you can use the traditional long multiplication method. Here’s how you can do it:

Let’s say you want to multiply a four-digit number, let’s call it “WXYZ,” by a three-digit number, let’s call it “UVW.”

  1. Write the numbers vertically, aligning them by place value.
    WXYZ
 x  UVW
 ------
  1. Start with the rightmost digit of the top number (the one place, “Z”), and multiply it by each digit of the bottom number. Write the partial products beneath each corresponding digit of the top number, shifted to the right according to their place value.
    WXYZ
 x  UVW
 ------
     P    <- Partial product (ones place)
    PP    <- Partial product (tens place)
   PPP    <- Partial product (hundreds place)
  PPP     <- Partial product (thousands place)
  1. Move to the next digit of the top number (the tenth place, “Y”), and repeat the process. Multiply it by each digit of the bottom number, and write the partial products beneath each corresponding digit of the top number, shifted to the right according to their place value.
    WXYZ
 x  UVW
 ------
     P    <- Partial product (ones place)
    PP    <- Partial product (tens place)
   PPP    <- Partial product (hundreds place)
  PPP     <- Partial product (thousands place)
+PPPP     <- Partial product (ten-thousands place)
  1. Repeat the process for the next digit of the top number (the hundreds place, “X”). Multiply it by each digit of the bottom number, and write the partial products beneath each corresponding digit of the top number, shifted to the right according to their place value.
    WXYZ
 x  UVW
 ------
     P    <- Partial product (ones place)
    PP    <- Partial product (tens place)
   PPP    <- Partial product (hundreds place)
  PPP     <- Partial product (thousands place)
+PPPP     <- Partial product (ten-thousands place)
-------
 RESULT   <- Final result
  1. Repeat the process for the leftmost digit of the top number (the thousand place, “W”). Multiply it by each digit of the bottom number, and write the partial products beneath each corresponding digit of the top number, shifted to the right according to their place value.
    WXYZ
 x  UVW
 ------
     P    <- Partial product (ones place)
    PP    <- Partial product (tens place)
   PPP    <- Partial product (hundreds place)
  PPP     <- Partial product (thousands place)
+PPPP     <- Partial product (ten-thousands place)
+PPPPP    <- Partial product (hundred-thousands place)
-------
 RESULT   <- Final result
  1. Add up all the partial products to get the final result.

Make sure to carry over any values that exceed nine during each step of the multiplication process.

Note: Replace “WXYZ” and “UVW” with the actual digits of the numbers you are multiplying.

Read More:

What do you learn?
  1. how to do 3 digit multiplication
  2. how to do 3 digit by 2 digit multiplication
  3. how do you do 3 git by 2 digit multiplication
  4. how do you do 3 digit by 3 digit multiplication
  5. multiplying 4 digits by 3 digits
  6. multiplying 3 digit by 1 digit
  7. multiplying 3 by 3 digit numbers
  8. multiply 4 digit by 3 digit
  9. shortcut multiplication 3 digit numbers
Photo of admin adminJanuary 15, 2024
0 28 12 minutes read
Photo of admin

admin

Related Articles

9 Best Talking Bird Species | Types of Pet Birds That Talk

July 25, 2022

15 Better Online slots games To own https://777spinslots.com/online-slots/vikings-unleashed-megaways/ Higher Winnings And you may Real money Wins

November 14, 2021

How to Make Money with Web Scraping using Python in 3 Steps

October 14, 2023
5 food groups

Nutrition Basics | Healthy Food | The 5 Food Groups Pyramid

March 29, 2021

Leave a Reply

Your email address will not be published. Required fields are marked *

Back to top button